粒子径は何でも丸い粒子として考えるのか
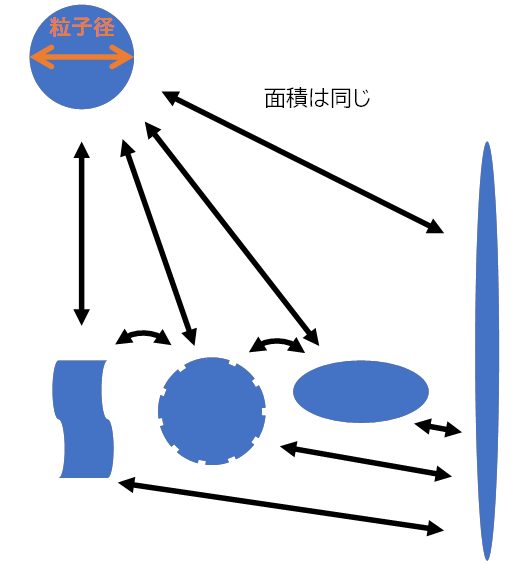
粒子径はまずは丸い粒子として考える、というお約束事を粒子と粒子径のページで話しました。 このため、上記のどの粒子も粒子径と言えば、オレンジの⇔が粒子径であることになります。
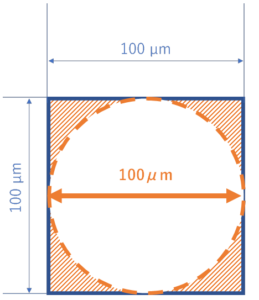
ですが、実際に粒子の大きさで↓のような直径100 μmの四角い粒子があったら、やっぱり粒子径は100 μmと考えてしまいそうです。
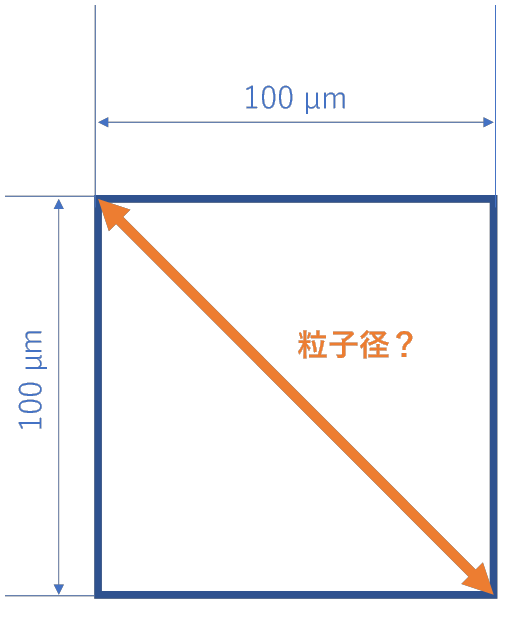
ただ、中には矢印とする人もいるかもしれません。
これらの考え方も間違いではありません。
粒子計測は実用から生まれているので、よりよいわかりやすく、便利な方法で考えても構わないのです。
ただ、上記の粒子を何も前提条件がなく、単に100μmと言ってしまうと、相手によっては下記のように▨の部分を無視した、ちょっと小さな粒子だと理解されてしますので、注意が必要です。
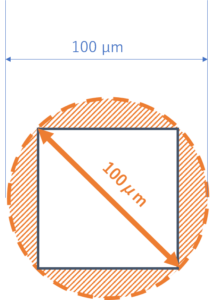
前提条件の話をもう少し続けます。
「対角線上に粒子径をとるなんて普通する? 」と思った方。 少し見方を変えて粒子をまわしてみましょう。
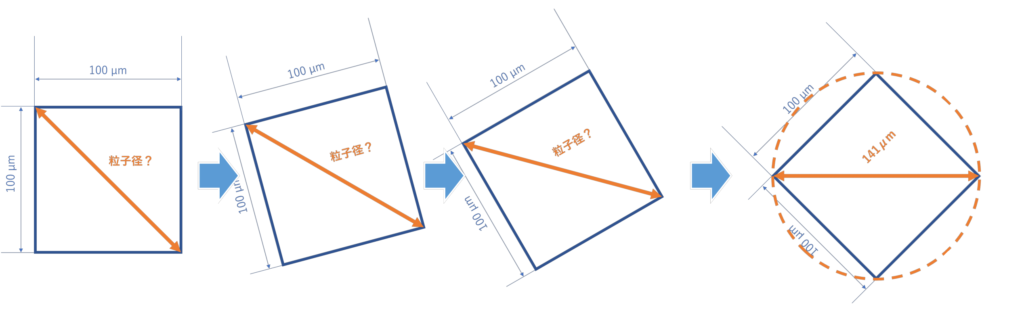
対角線を粒子径とするのもありうる、そう思えてきませんか?
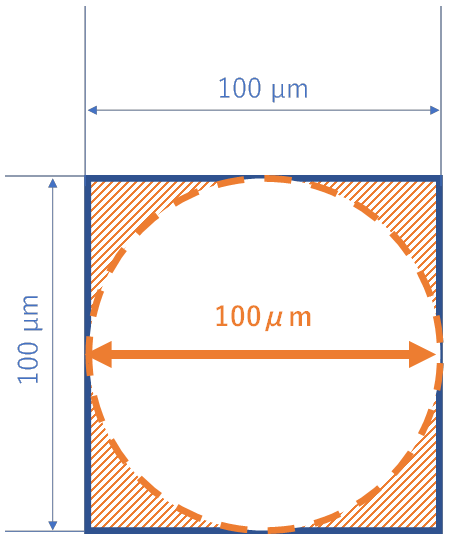
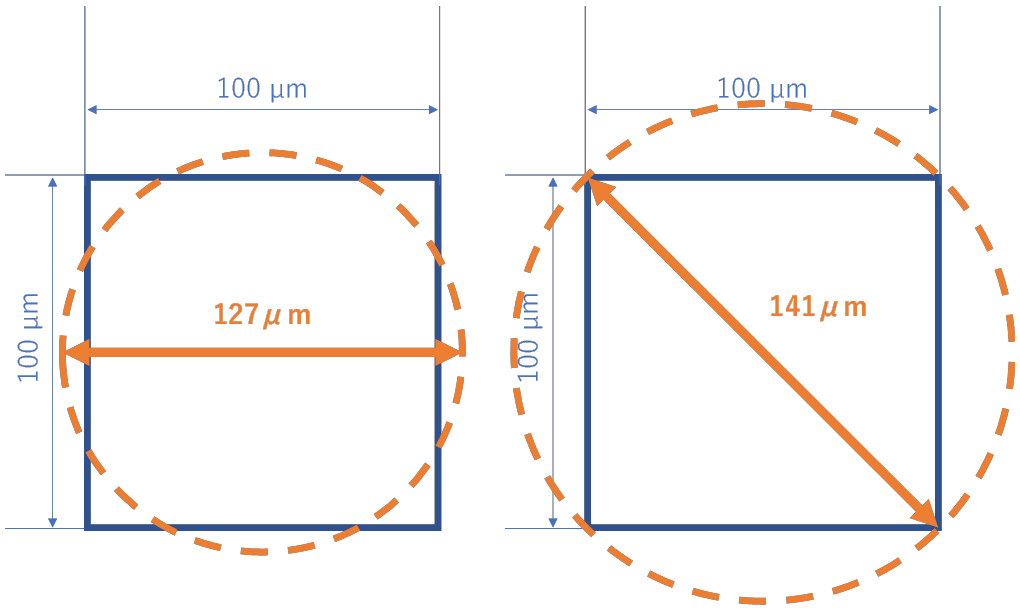
このように、□の一辺が100μmでも前提条件を統一しないと、▨分を無視した丸い直径100μmの粒子ととらえる人が出てきてしまったりすることがあります。 逆に、□の1辺が100μmの粒子もとらえ方を変えると、面積が同じ丸い粒子の直径、ということで127μmの粒子と認識してしまったり、対角線の長さで141μmと考えてしまったりすることもあり得ます。 つまり何を前提としての粒子径なのかをはっきりさせておかないと、議論が成り立たなくなってしまうのです。
さまざまな粒子をすべて球(写真だと円)としてもよいのか?
このページの初めに出てきた5つの粒子はどれも面積が同じなので⇔の円相当径で示すことができる、ということは既にお知らせしたとおりですが、本当に同じように評価をしていてよいのでしょうか?
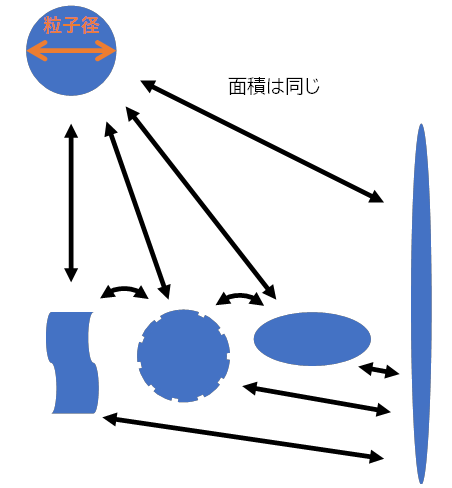
粒子が丸いか丸くないかは製造上の理由で決まってくることも多いのですが、粒子にある機能を付与するために、わざと丸くない粒子を製造することもあります。
例えば上記の同じ粒子径を示すことができる5つの粒子でそれぞれ丸くないことに意味があったとします。
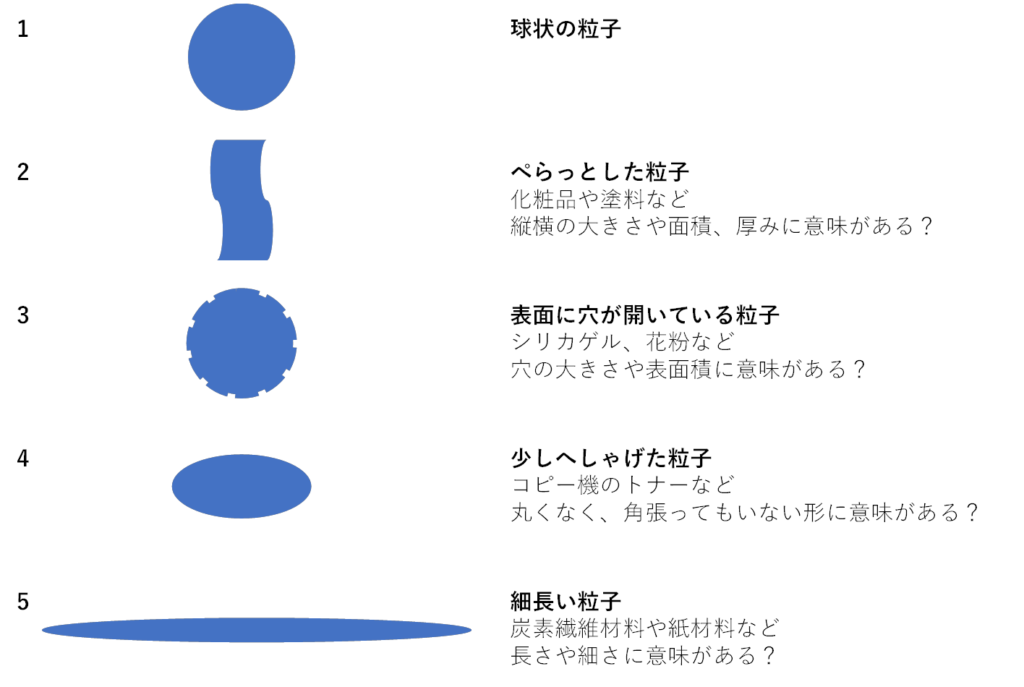
これら2~5の粒子は、丸い粒子として数値化してしまうことに意味がなくなってしまいます。 ではどうすれば意味のある評価ができるのでしょうか。
その粒子を特徴づけられる方法で粒子の大きさを表現すればよいのです。 粒子径の考え方は前提条件が大事、という話は既にしましたが、前提条件によって粒子径に名前がつけられています。
これをちょっと複雑な形の粒子で説明してみます。
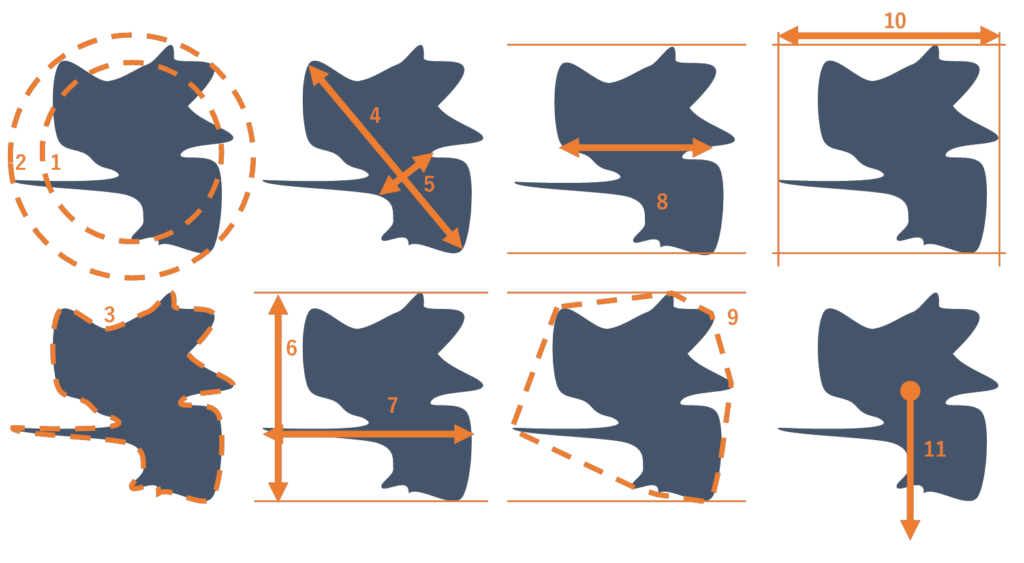
粒子径の考え方にはいろいろありますが、なぜ基本は丸いものとして考えるのか?
それは、粒子径を測定する様々な機器で、球を前提とした値を算出するためです。
いろいろな粒子径から、形状を数値化する
場合によっては粒子径の評価だけでは情報が不足しており、形そのものを評価する必要があります。
そのため、粒子形状を数値化することが必要になります。 そこで、様々な考え方での粒子径を掛け合わせて、形状を数値化していきます。 ここでも、目的に合わせてどの形状パラメータが最もその粒子の状態を表現できるのかを考える必要があります。
大体どの方法でも完全な真球(または2次元的に見て真円)であれば、数値化すると1となり、0に近づけば近づくほど、球から程遠い形状ということになります。
粒子像と形状
粒子の形状を表現するには、粒子の像そのものから粒子径を評価する必要があります。 他の方法で計測した場合だと、球換算された値が表示されてしまうからです。
ただ、光学顕微鏡で粒子を観察できるのはせいぜい数μm以上の粒子、それ以下になると電子顕微鏡が必要になってきます。 電子顕微鏡は安くても数100万円以上する非常に高価な装置ですが、それ以上に撮影するための技術や慣れが必要になります。 例えば粒子のどこにピントを合わせるかによって粒子径が変わってしまったり、かといってのんびり視野を探していると粒子が電子線で壊れてしまったりしてしまうことがあるためです。
また、光学顕微鏡・電子顕微鏡を問わず、1枚の写真では数個~数10個の粒子しか撮像できないため、統計学的に有意な粒子数を分析しようとすると大量の写真が必要になる、また1粒子ごとの解析にも非常に時間がかかるので、必要がなくてもとりあえず何でも形状を分析する、というのはお勧めできません。
