主成分分析とは何なのか
本稿では、主成分分析(PCA:Principal Component Analysis)とは何なのか、なぜあんなややこしい計算を行うのか、いったい何をやってるのか、どんなコンセプトなのか、どのように理解すれば良いのか考えてみます。
はじめに
例えば下表のような2次元データがあり、データ数を減らしたいニーズがあるとします。条件はできるだけデータの特徴を維持しつつです。
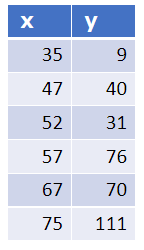
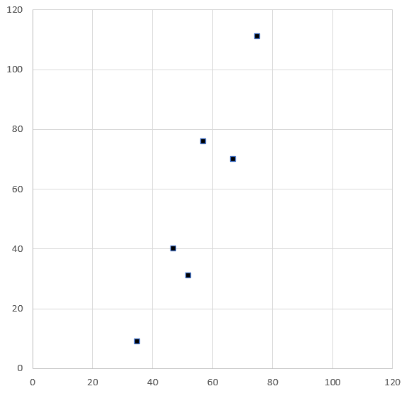
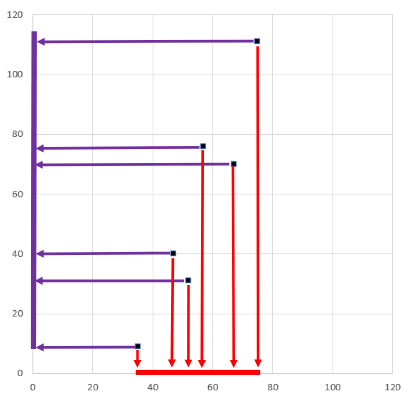
仮にyのデータをすべて捨てて、xだけ残す場合はどうでしょう。2次元データはグラフ2のx軸に張り付いた赤線で表現されます。一方、xのデータをすべて捨ててyだけ残す場合はどうでしょう。2次元データはグラフ2のy軸に張り付いた紫線で表現されます。(それぞれx軸やy軸にデータを射影している。)で、どちらが元の特徴を維持していると考えるか、選択するかというと、yのデータを残す方を選択すると思います。これは直感的にバラツキが多いほうを残すべきと考えているのでしょう。
ところで、射影すべき軸はx軸とy軸だけかというとそんなことはりません。グラフ3のような軸が考えられます。データのバラツキが最大になるような軸を探すことが主成分分析です。
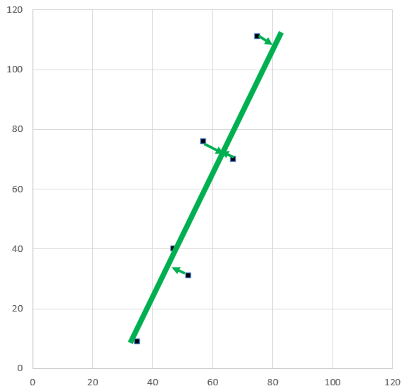
主成分分析が何の役に立つのか
データの特徴を把握するのに役立ちます。主成分がわかれば主成分じゃないデータを削除すれば特徴をおおむね維持しつつデータ量を圧縮できます。データの次元数を削減できることで複雑なデータを可視化したり把握が容易になります。
<寄り道>
課題を解き進めるために2つ寄り道します。固有値と固有ベクトル、そして、ラグランジュの未定乗数法です。
固有値と固有ベクトル
ある行列Aがあって、ベクトルxに行列Aを左からかけたとき、ベクトルxの向きは変わらず大きさだけかλ倍になるような、ベクトルxとλの組を求めることを、固有ベクトルと固有値を求めると言います。固有ベクトルに行列Aを左からかけた時の値と、固有ベクトルにλをかけた場合の値とが同じになるという特殊なことが起こります。こういう特殊なケースを探すことが固有値問題です。主成分分析の中で登場します。
先ずは定義から。

例題を解いてみましょう。


ラグランジュの未定乗数法
これも寄り道。主成分分析の中で登場します。
これも定義から。

こちらも例題を解いてみましょう。

寄り道から戻ります。
主成分分析
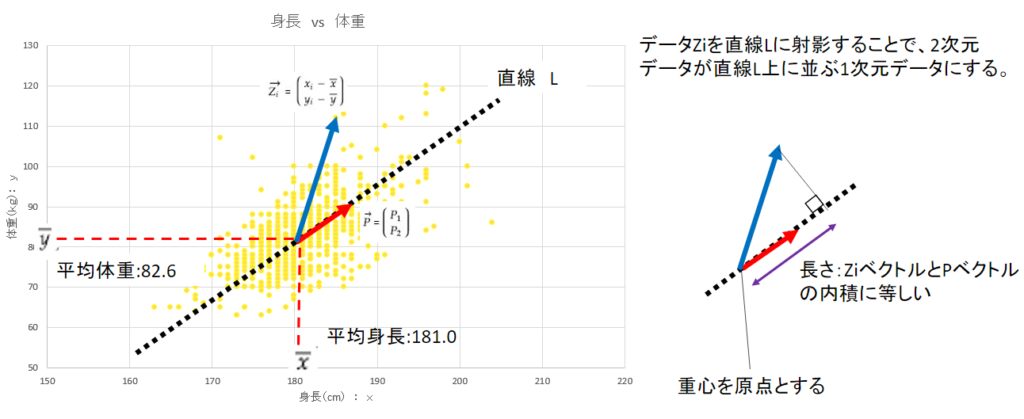
理解を簡単にするために、2次元のデータにおける主成分分析を考えてみましょう。n人についてxとy、例えば、身長と体重のデータがあるとします。以下の図のように2次元で表現できます。ドットひとつはn人のうちの誰かのデータを示しています。ベクトル表記だとi番目のデータは、Ziベクトル(下図の式(1))のように表現できます。
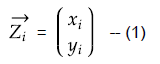
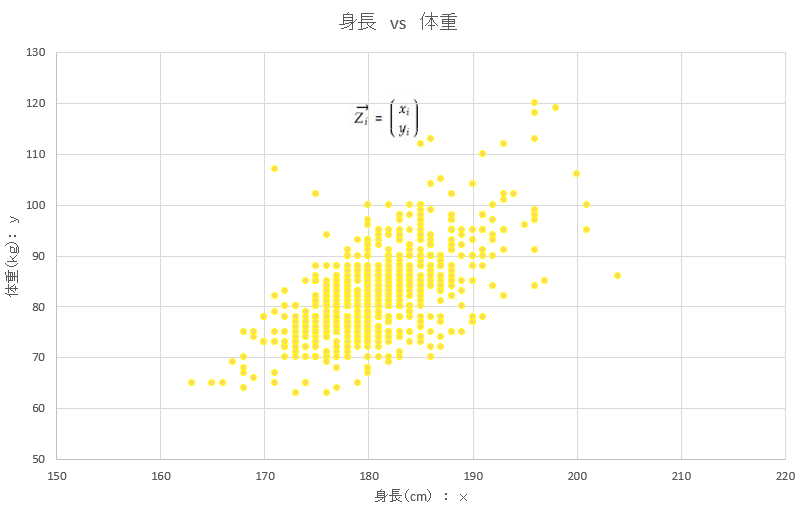
この2次元データを1次元データに次元削減するとしたら、つまり、直線上に並ぶデータにするとしたら、その線はどんな風に描画できるでしょうか。この図では、右斜め方向にデータが大きくばらついているので、そのような向きに引かれる直線上に元データが射影すれば、元の特徴(バラツキ)をそれなりに維持しつつ、次元削減できそうです。その直線を数学的に求めていきます。直線をl(エル)とします。
直線は重心(身長の平均値、体重の平均値)を通ります。
ここで、あるデータのベクトルZiを身長と体重が0の点を中心とした座標で表現するのではなく、上記の重心を原点として表現するとデータは重心からの偏差で表現します。式(2)
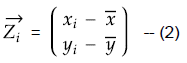
そして直線上の原点(=データの重心)から長さ1の単位ベクトルをPとします。式(3)
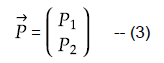
Ziベクトルの直線lへの射影は、ZiベクトルとPベクトルの内積をとることで求められます。
ZiベクトルとPベクトルの内積は、ZiがどれだけPベクトル方向に働いているかを示します。
ZiベクトルとPベクトルの内積(式(4))は、転置を用いて次のように式(5)のように変形できます。
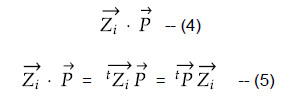
ところで、バラツキは分散と呼ばれ、個々のデータと平均値との差について二乗和をデータ数で割った式(二乗和平均)で表現されました。
先のZiとPの内積の二乗和平均が最大となる条件を探っていくことにします。つまり、Pベクトルへ射影したときの分散を求めていく、それが最大となる条件を探ることになります。
先ずは ZiとPの内積の二乗を式(5)の変形を用いながら表現し、その後で分散を求める式へ展開します。
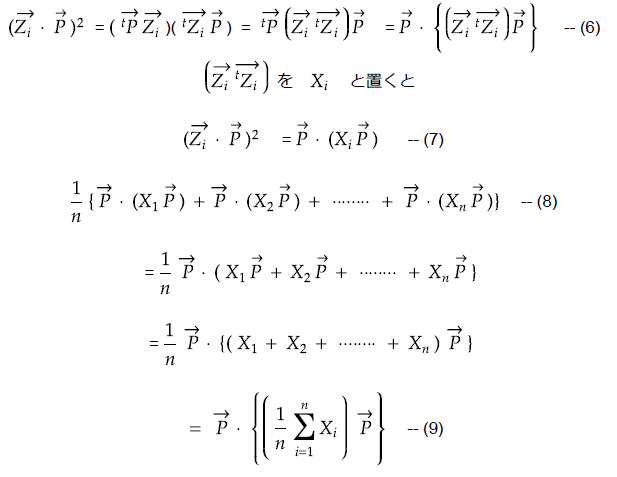
ベクトルの成分で表現してみましょう。
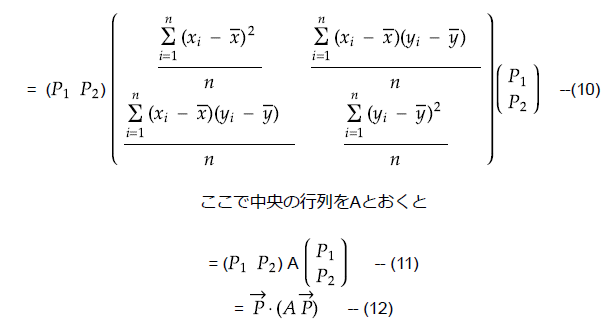
行列Aは分散共分散行列と呼ばれています。
主成分を分析するのに、データのバラツキが大きくなる条件を探ってきました。このバラツキの大きさ、分散は、式(12)で表すことができましたので、主成分分析は、この式(12)を最大となるようなベクトルPを求めていくことになりました。
式(12)が最大となるPベクトルを求めるには、どうすれば良いでしょうか。
ある制約条件(束縛条件)のもとで、関数の最大(最小)を決定する時には、「ラグランジュの未定乗数法」というものがよく用いられるので、これを使って、 式(12)が最大となるPベクトルを求めます。

先に示した分散共分散行列Aの固有方程式となっていることがわかりました。Pベクトルは分散共分散行列A の固有ベクトルであり、λは固有値です。
これにより、データの二乗和平均が最大になるような座標軸(方向)は、データの分散共有分散行列の固有値が大きい側の固有ベクトルに平行な方向(主成分や主方向と呼ぶ)だということが分かりました。
主成分分析を行うことは、分散共分散行列の最大固有値を見つけそれに対応する固有ベクトルを主成分と考えることです。主成分分析は固有値問題だいうことが分かります。
忘れそうなので早めに手順を振り返ります。
データの重心を求めます。
その重心とデータの偏差を考えて二乗和の平均(=分散共分散行列)が最大となる軸の方向を求めます。この軸の方向を求めることは、分散共分散行列の固有値や固有ベクトルを求めることとに等しいことが分かりました。
今回の例(2行2列の行列)では固有値は2つあります。大きい方の固有値に対する固有ベクトルが主成分で、もう一つの固有値に対する固有ベクトルは第2主成分と呼ばれます。主方向の次にバラツキが大きい方向です。
これらのベクトルは直交しています。
ところで、先ほど登場したデータは身長と体重で示されるデータでした。上記で求めた主成分は、新しく見出した指標です。これを”ガタイ”としましょうか。 他方は、”肥満度”にしましょうか。主成分だけでデータを表現すれば、ほどほどに元のデータの特徴を維持しつつ次元削減できそうです。
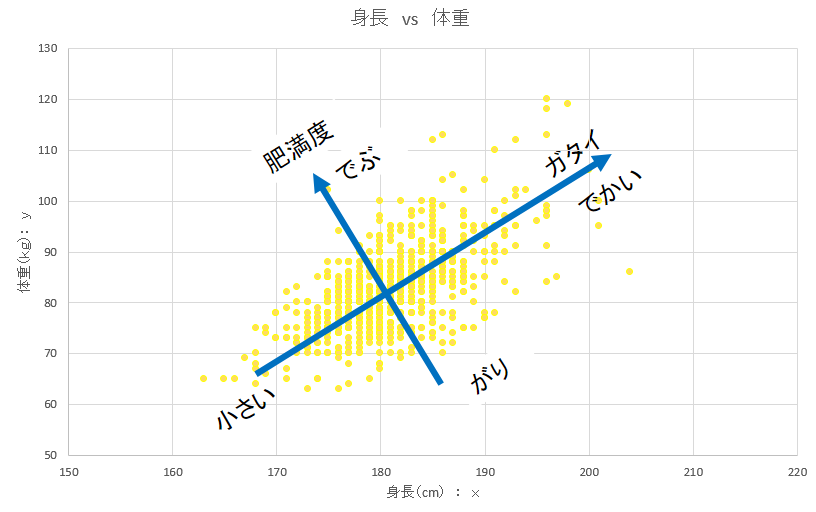
さて、次元削減は置いておいて、新しい座標系での表現に変わったことに着目しましょう。
元の身長(x)と体重(y)という指標で表現していたデータは、新たな指標・新たな座標軸で表現し直されました。その主成分ベクトルと第2成分ベクトルはそれぞれ直交基底ベクトルです。データは直交基底ベクトルで表現されるようになったわけですが、同じような直交系の仲間を思い出しませんか。
時系列データを周波数の異なるSIN波とCOS波の和で表現できるフーリエ解析です。
こちらにまで手を出せば、ベクトルという考え方の便利さをもっと理解できそうですが、疲れてきたので、本稿はここまでにしておきます。


